Translate

Jumat, 11 April 2014

Mentari

Hai mentari
Apa kabarmu hari ini?"
Kini ceritaku berbeda
Langkahku selalu ada bayangmu
Hai mentari
Roda kehidupan kini kurasa
Putaran yang tak selamanya cepat
Atau kian melambat
Hai mentari
Inilah arti hidup
Terikmu yang selalu setia menemaniku
Usia ku kini tak lagi kanak-kanak
Lihat dibalik ragaku
Ada sesosok Ibu
Ibu yang tak lepas mendoakanku
Hai mentari
Ucapkan rinduku untuk sahabat-sahabat diluar sana

Semoga kesuksesan meyertai kita semua :)

Diposting oleh di Tidak ada komentar:

Senin, 08 April 2013

Teruntuk Sahabat d'm3+d'matriks (Milla, Fitri, Alan, Amin dan Andi)

sahabat..
ketika ku terdiam sendiri
mengingat hari-hari yang aku jalani

ketika kepercayaan selalu melekat dalam diri
tta' ada pemisah atapun penghalang
sahabat yang begitu dekat
menjadi kawan tanpa batas

 genap empat tahun kita bersama
dimulai dari perkenalan
belajar, hangout, suka hingga duka

 sahabat,.
empat tahu silam awal kita bersama
karna bagiku kalian teman, sahabat, hingga keluargaku
 sekarang kita sudah dipuncak pembelajaran
dapatkah kita bersama?"

teruntuk sahabat-sahabatku diluar sana
sukses dan pantang menyerah
ingat keluarga jikalau kita berhenti untuk melangkah
karna tujuan kita sukses tidak lan dan bukan hanya untuk membahagiakan orang tua,

sukses untuk kalian semua...
d'm3 + d'matriks
Hangatnya kebersamaan


Jogjakarta, 4 November 2010

 
Perjalanan setelah perayaan ulang tahun Vhie
Majalengka, 17 April 2012








  Perayaan ulang tahun Alan
Cirebon, 10 November 2011











Cilengkrang, 7 Februari 2012





Diposting oleh di Tidak ada komentar:

Selasa, 27 November 2012

metode numerik : metode secant

metode secant

Pada Metode Newton-Raphson memerlukan syarat wajib yaitu fungsi f(x) harus memiliki turunan f’(x). Sehingga syarat wajib ini dianggap sulit karena tidak semua fungsi bisa dengan mudah mencari turunannya. Oleh karena itu muncul ide dari yaitu mencari persamaan yang ekivalen dengan rumus turunan fungsi. Ide ini lebih dikenal dengan nama Metode Secant. Ide dari metode ini yaitu menggunakan gradien garis yang melalui titik (x0, f(x0)) dan (x1, f(x1)). Perhatikan gambar dibawah ini.
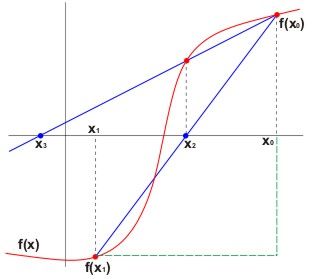
Photobucket
Persamaan garis l adalah
\frac{x-x_1}{x_0-x_1} = \frac{y-f(x_1)}{f(x_0)-f(x_1)}
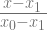
Karena x = x2 maka y = 0, sehingga diperoleh
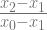
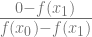
\frac{x_2-x_1}{x_0-x_1} = \frac{0-f(x_1)}{f(x_0)-f(x_1)}
x2 – x1 = -\frac{f(x_1)[x_0-x_1]}{f(x_0)-f(x_1)}
x2 = x1 – \frac{f(x_1)[x_0-x_1]}{f(x_0)-f(x_1)}
= x1 – \frac{f(x_1)[x_1-x_0]}{f(x_1)-f(x_0)}
secara umum rumus Metode Secant ini ditulis
xn+1 = xn – \frac{f(x_n)[x_n-x_{n-1}]}{f(x_n)-f(x_{n-1})}
Prosedur Metode Secant :
Ambil dua titik awal, misal x0 dan x1. Ingat bahwa pengambilan titik awal tidak disyaratkan alias pengambilan secara sebarang. Setelah itu hitung x2 menggunakan rumus diatas. Kemudian pada iterasi selanjutnya ambil x1 dan x2 sebagai titik awal dan hitung x3. Kemudian ambil x2 dan x3 sebagai titik awal dan hitung x4. Begitu seterusnya sampai iterasi yang diingankan atau sampai mencapai error yang cukup kecil.
Contoh :

Tentukan salah satu akar dari 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Secant sampai 9 iterasi.
Penyelesaian :

f(x) = 4x3 – 15x2 + 17x – 6
iterasi 1 :
ambil x0 = -1 dan x1 = 3 (ngambil titik awal ini sebarang saja, tidak ada syarat apapun)
f(-1) = 4(-1)3 – 15(-1)2 + 17(-1) – 6 = -42
f(3) = 4(3)3 – 15(3)2 + 17(3) – 6 = 18
x2 = (3) – \frac{(18)[3-(-1)]}{18-(-42)} = 1.8
iterasi 2 :
ambil x1 = 3 dan x2 = 1.8
f(1.8) = 4(1.8)3 – 15(1.8)2 + 17(1.8) – 6 = -0.672
x3 = (1.8) – \frac{(-0.672)[1.8-(3)]}{-0.672-18} = 1.84319
iterasi 3 :
ambil x2 = 1.8 dan x3 = 1.84319
f(1.84319) = 4(1.84319)3 – 15(1.84319)2 + 17(1.84319) – 6 = -0.57817
x4 = (1.84319) – \frac{(-0.57817)[1.84319-1.8]}{-0.57817-(0.672)} = 2.10932
iterasi 4 :
ambil x3 = 1.84319 dan x4 = 2.10932
f(2.10932) = 4(2.10932)3 – 15(2.10932)2 + 17(2.10932) – 6 = 0.65939
x5 = (2.10932) – \frac{(0.65939)[2.10932-1.84319]}{0.65939-(-0.57817)} = 1.96752
iterasi 5 :
ambil x4 = 2.10932 dan x5 = 1.96752
f(1.96752) = 4(1.96752)3 – 15(1.96752)2 + 17(1.96752) – 6 = -0.15303
x6 = (1.96752) – \frac{(-0.15303)[1.96752-2.10932]}{-0.15303-0.65939)} = 1.99423
iterasi 6 :
ambil x5 = 1.96752 dan x6 = 1.99423
f(1.99423) = 4(1.99423)3 – 15(1.99423)2 + 17(1.99423) – 6 = -0.02854
x7 = (1.99423) – \frac{(-0.02854)[1.99423-1.96752]}{-0.02854-(-0.15303)} = 2.00036
iterasi 7 :
ambil x6 = 1.99423 dan x7 = 2.00036
f(2.00036) = 4(2.00036)3 – 15(2.00036)2 + 17(2.00036) – 6 = 0.00178
x8 = (2.00036) – \frac{(0.00178)[2.00036-1.99423]}{0.00178-(-0.02854)} = 2.00000
iterasi 8 :
ambil x7 = 2.00036 dan x8 = 1.999996
f(1.999996) = 4(1.999996)3 – 15(1.999996)2 + 17(1.999996) – 6 = -0.0002
x9 = (1.999996) – \frac{(-0.0002)[1.999996-2.00036]}{-0.0002-0.00178} = 2.0000
iterasi 9 :
ambil x8 = 1.999996 dan x9 = 2.00000
f(2.00000) = 4(2.00000)3 – 15(2.00000)2 + 17(2.00000) – 6 = 0.00000
x10 = (2.00000) – \frac{(0.00000)[2.00000-1.999996]}{0.00000-(-0.00002)} = 0.00000
n
 xn-1
 xn
 xn+1
 f(xn-1)
 f(xn)
 f(xn+1)
1
2
3
4
5
6
7
8
9
 -1
3
1.8
1.84319
2.10932
1.96752
1.99423
2.00036
2.00000
 3
1.8
1.84319
2.10932
1.96752
1.99423
2.00036
2.00000
2.00000
 1.8
1.84319
2.10932
1.96752
1.99423
2.00036
2.00000
2.00000
2.00000
 -42
18
-0.672
-0.57817
0.65939
-0.15303
-0.02854
0.00178
-0.00002
 18
-0.672
-0.57817
0.65939
-0.15303
-0.02854
0.00178
-0.00002
0.00000
 -0.672
-0.57817
0.65939
-0.15303
-0.02854
0.00178
-0.00002
0.00000
0.00000
Jadi salah satu akar dari 4x3 – 15x2 + 17x – 6 = 0 adalah 2
selanjutnya dapat di lihat
www.iaincirebon.ac.id/tmtk
www.fitthree16.blogspot.com
www.millatulkhaniifah28.blogspot.com
Diposting oleh di Tidak ada komentar:

METODE NUMERIK: Pengertian dan Kegunaan Metode Numerik

 Pengertian dan Kegunaan Metode Numerik

Beberapa definisi metode numerikdikemukakan ahli matematika, misalnya metode numerik adalah teknik dimana masalah matematika diformulasikan sedemikian rupa sehingga dapat diselesaikan oleh pengoperasian aritmetika (Chapra dan Chanale, 1991); metode numerik adalah teknik -teknik yang digunakan untuk merumuskan masalah matematika agar dapat diselesaikan han ya dengan operasi hitungan, yang terdiri dari operasi tambah, kurang, kali dan bagi (Susila, 1994 ; Ibraheem dan Hisyam, 2003). Terdapat banyak jenis metode numerik, namun pada dasarnya, masing -masing metode tersebut memiliki karakteristik umum, yaitu selalu mencakup sejumlah kalkulasi aritmetika. Jadi metode numerik adalah suatu teknik untuk memformulasikan masalah matematika sehingga dapat diselesaikan dengan operasi aritmetika yang terdiri dari operasi tambah, kurang, kali dan bagi (Rochmad, 2011).
Di samping itu menurut Rochmad (2011) ada sejumlah alasan mengapa orang menggunakan metode numerik untuk memecahkan masalah yang dihadapinya.  Beberapa alasan tersebut sebagai berikut.
  1. Metode numerik merupakan suatu teknik untuk menyelesaikan masalah matematika yang efektif dan efisien. Dengan bantuan komputer ia sanggup menangani masalah yang rumit dan melibatkan perhitungan y ang luas, misalnya untuk memecahkan masalah solusi suatu persamaan tak linear, sistem persamaan yang besar, dan permasalahan lainnya termasuk dalam teknik dan sosial.  Masalah yang sering sulit atau bahkan tidak mungkin dapat diselesaikan secara analitis dapat diselesaikan dengan metode numerik.
  2. Saat ini terdapat berbagai paket program komputer (misalnya exel, maple, matlab, atau program paket lainnya) yang tersedia dan diperdagangkan sehingga mudah didapat yang dalam pengoperasiannya mencakup metode numerik. Dengan demikian, pemecah masalah tinggal menyesuaikan dengan karakteristik program paket tersebut dengan algortima yang digunakan dalam pemecahan masalah.
  3. Apabila masalah yang dihadapi sulit diselesaikan dengan bantuan program paket komputer, maka pemecah masalah dapat menggunakan program komputer (misalnya basic, pascal, fortran, atau  program komputer lainnya). Jika pemecah masalah mahir mendesain program sendiri, maka pemecah masalah dapat lebih leluasa dalam menggunakan metode numerik untuk memecahka n masalah yang dihadapinya.
  4. Di sisi lain, metode numerik merupakan semacam sarana  yang efisien untuk mengenal karakteristik komputer dan mendesain algoritma, diagram alur dan menulis program komputer sendiri.
selanjutnya dapat dilihat di : 
www.iaincirebon.ac.id/tmtk
www.fitthree16.blogspot.com
www.millatulkhaniifah28.blogspot.com
Diposting oleh di Tidak ada komentar:

Rabu, 21 November 2012

Metode Numerik

Tujuan dan Manfaat Eliminasi Gauss - Jordan
Tujuan:
Manfaat:
1. Membantu memahami lebih lanjut penyelesaian sistem persamaan linier dengan metode eliminasi Gauss-Jordan.
2. Membantu penyelesaian persamaan Linier
Membantu pengguna yang ingin menyelesaikan sistem persamaan linier.
3. Membantu mempelajari langkah-langkah yang dilakukan untuk menyelesaikan sistem persamaan linier.
SEJARAH
Wilhelm Jordan (1842-1899) adalah seorang insinyur Jerman yang ahli dalam bidang geodesi. Sumbangannya untuk penyelesaian sistem linear dalam buku populernya, Handbuch de Vermessungskunde (Buku panduan Geodesi) pada tahun 1988.
Contoh Sumbangannya untuk penyelesaian sistem linear dalam buku populernya dalam aljabar linear, eliminasi Gauss-Jordan adalah versi dari eliminasi Gauss.
Pada metode eliminasi Gauus-Jordan kita membuat nol elemen-elemen di bawah maupun di atas diagonal utama suatu matriks. Hasilnya adalah matriks tereduksi yang berupa matriks diagonal satuan (Semua elemen pada diagonal utama bernilai 1, elemen-elemen lainnya nol).
Motede tersebut dinamai Eliminasi Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Whilhelm Jordan.
Eliminasi Gauss adalah suatu metode untuk mengoperasikan nilai-nilai  didalam matriks sehingga menjadi matriks yang lebih sederhana lagi.
Caranya dengan mengubah persamaan linear
tersebut ke dalam matriks teraugmentasi dan
mengoperasikannya. Setelah menjadi matriks baris,
lakukan substitusi balik untuk mendapatkan nilai
dari variabel-variabel tersebut.
Eliminasi Gauss-Jordan juga merupakan  pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana lagi.
Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan matriks yang Eselon-baris. Ini juga dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks.

Ciri – ciri Eliminasi Gauss – Jordan
1. Entri-entri dalam sebuah baris tidak semuanya nol, maka entri pertama yang tidak nol harus 1 (disebut 1-utama / leading-1)
2. Baris-baris yang semua entrinya 0, dikelompokkan di bagian bawah matriks
3. Posisi 1-utama dari baris yang lebih bawah harus lebih ke kanan daripada 1-utama baris yang lebih atas
4. Semua entri (yang lain) dari kolom yang berisi 1-utama harus di-0-kan

Algoritma Metode Eliminasi Gauss-Jordan
1. Tulis sistem persamaan dalam matrik augmentasi (matrik lengkap) [A|B]
2.Ubah matrik lengkap kedalam bentuk:
[A|B] → [I|C] dimana I adalah matrik identitas
3. Ketika langkah kedua sudah terpenuhi, tulis
matriks [I|C] sebagai hasil akhir persamaan
Ciutkan pos ini
www.iaincirebon.ac.id/
Diposting oleh di Tidak ada komentar:

Kamis, 26 April 2012

Hartaku, Sahabatku

Angan harap
Impian masa depan
Senja yang tta' lagi jingga
Dan fajar yang tta' lagi cerah
Ku melangkah,
Berbekal semangad tuk meraih cita-cita
Sahabat
Yang tlah lama bersama
Mengantarkan fajar hingga senja
Matahari terus bersinar
Debaran angin dan derasnya hujan
Tta' bisa menghalangi persahabatan kita
Cirebon, 7 Februari 2012
Diposting oleh di Tidak ada komentar:
Langganan: Postingan (Atom)